728x90

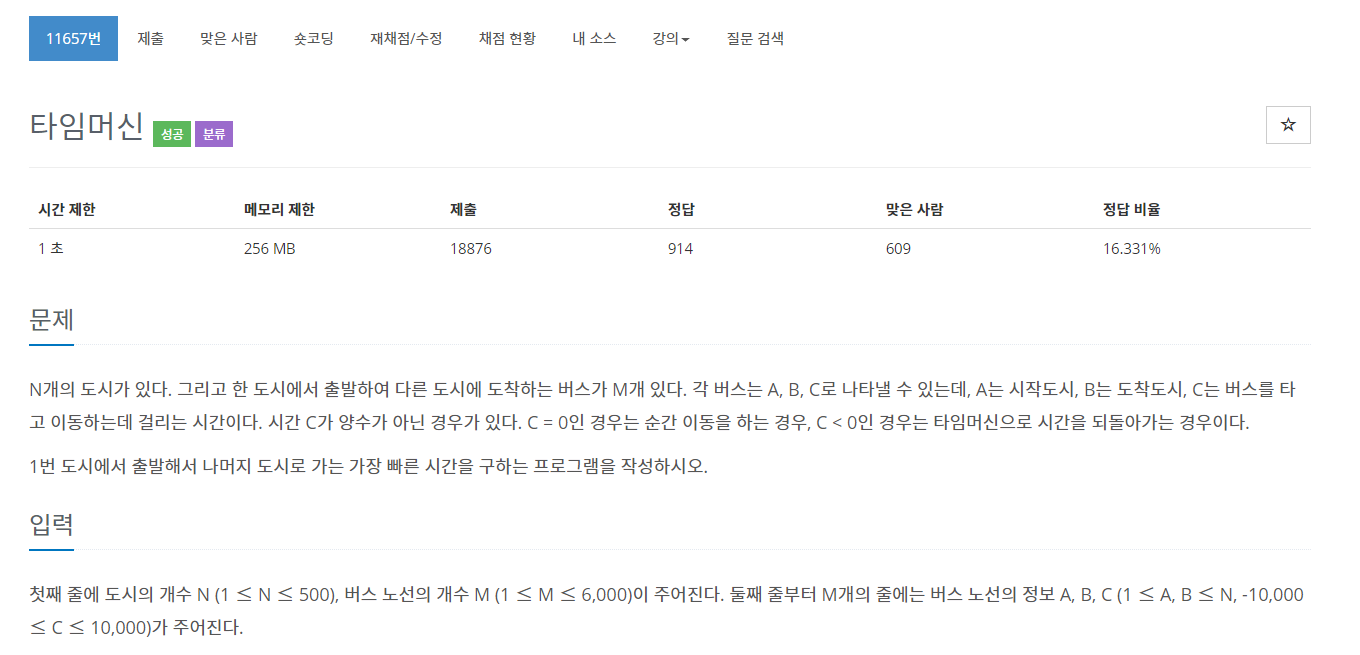

☞ 이 문제에서는 음수 간선이 존재하며, 출력 내용에서의 "만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다." 를 보면 그래프에 음수 사이클이 존재하는 경우 -1을 출력하라는 말이라고 볼 수 있다.
따라서 음수간선이 존재하며 음수 사이클의 존재를 판단 할 수 있는 '벨만-포드 알고리즘'을 사용하면 된다.
'벨만-포드 알고리즘'은 아래에 잘 설명이 되어있으니 참고해주세요.
https://withseungryu.tistory.com/34
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
☞ 그래프의 최단 경로를 알고 싶고, 그래프에 음수 간선이 있으며, 음수 사이클이 존재 할 때 다익스트라 알고리즘을 사용해 최단 경로를 구해도 될까? -> 정당성에 성립되지 않습니다. 따라서 �
withseungryu.tistory.com
위 글을 보고 벨만-포드 알고리즘만 쉽게 작성 할 수 있다면, 손쉽게 이 문제를 해결 할 수 있다.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N, M;
vector<pair<int, int>> adj[502];
vector<long long> bellmanFord(int src) {
vector<long long> upper(N+1, 99999999);
upper[src] = 0;
bool updated;
for (int iter = 1; iter <= N; ++iter) {
updated = false;
for (int here = 1; here <= N; ++here) {
for (int i = 0; i < (int)adj[here].size(); ++i) {
int there = adj[here][i].first;
int cost = adj[here][i].second;
if (upper[there] > upper[here] + cost && upper[here] != 99999999 && here!=there) {
upper[there] = upper[here] + cost;
updated = true;
}
}
}
if (!updated) break;
}
if (updated) upper.clear();
return upper;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N >> M;
for (int i = 0; i < M; ++i) {
int a, b;
int c;
cin >> a >> b >> c;
adj[a].push_back(make_pair(b, c));
}
vector<long long> res = bellmanFord(1);
if (res.size() == 0) {
cout << -1;
}
else {
for (int i = 2; i < (int)res.size(); ++i) {
if (res[i] == 99999999) {
cout << -1;
}
else cout << res[i];
if (i != res.size() - 1) cout << endl;
}
}
}
소스코드: https://github.com/withseungryu/Algorithms
궁금하신 것이 있으시다면 댓글로 남겨주세요!~

728x90
반응형
'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [백준] 13900번 - 순서쌍의 곱의 합 (부분합) (0) | 2020.08.05 |
|---|---|
| [백준] 17070번 - 파이프 옮기기 1 (0) | 2020.08.02 |
| [백준] 2014번 - 소수의 곱 (0) | 2020.05.14 |
| [백준] 6593번 - 상범 빌딩 (0) | 2020.04.30 |
| [백준] 5014번 - 스타트링크 (0) | 2020.04.29 |
