
https://www.acmicpc.net/problem/2213
2213번: 트리의 독립집합
첫째 줄에 트리의 정점의 수 n이 주어진다. n은 10,000이하인 양의 정수이다. 1부터 n사이의 정수가 트리의 정점이라고 가정한다. 둘째 줄에는 n개의 정수 w1, w2, ..., wn이 주어지는데, wi는 정점 i의 ��
www.acmicpc.net
💡 원리
트리의 정점에 가중치가 있으며, 독립집합을 찾는 문제이다.
문제를 잘 읽어보면 트리의 동적 프로그래밍을 사용하면 풀리는 문제인데,
이 문제는 더 나아가 출력으로 가장 큰 독립집합의 값의 정점을 찾아 출력을 해야한다.
우선 동적 프로그래밍을 사용해 가장 큰 독립집합을 찾아보자
트리의 형태이기 때문에 root=0 부터 차례대로 정점을 탐색할 수 있고,
동적 프로그래밍을 계획해 최대 값을 갖고 오자
동적 계획
1) 정점이 독립 집합에 속해 있으면 다음 정점은 독립 집합에 속해 있으면 안되고,
2) 정점이 독립 집합에 속해 있지 않으면 다음 정점은 독립 집합에 속해 있어도 되고, 없어도 된다.

아래와 같이 dp[number][inv] 로 메모이제이션을 하면 메소드를 만들어주면 된다.
int getSet(int number, bool inv) {
int &ret = dp[number][inv];
if (ret != -1) {
return ret;
}
if (inv) {
ret = weight[number];
for (int i = 0; i < arr2[number].size(); ++i) {
int there = arr2[number][i];
ret += getSet(there, false);
}
}
else {
ret = 0;
for (int i = 0; i < arr2[number].size(); ++i) {
int there = arr2[number][i];
ret += max(getSet(there, true), getSet(there, false));
}
}
return ret;
}
여기까지는 많이 보았던 트리에서의 동적 프로그래밍을 푸는 방식이다.
하지만 이 문제는 최대 가중치를 갖는 독립 집합에 속하는 정점들도 나열해야 되기 때문에 다른 문제보다 까다로웠다.
어떻게 독립 집합의 정점들을 갖는 배열을 만들 수 있을까?
우선 메모이제이션을 사용했던 dp를 이용해야한다.
아래 그림에서 dp를 보자.
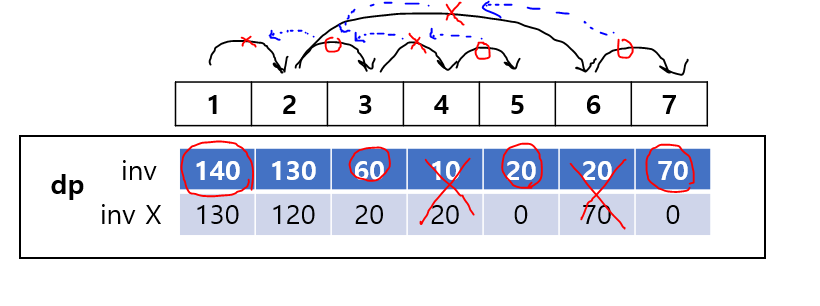
일단 최대 값의 독립 집합의 정점들은 dp의 inv의 값이 inv X의 값보다 더 커야 속 할 수 있다.
또한 독립 정점의 특징인 독립 집합에 속한 정점과 연결 된 값은 독립 정점의 값이 될 수 없는 조건도 추가해야 한다.
따라서 조건은
1) dp[number][inv] > dp[number][inv X]
2) visited[prev_number] == false
될 수 있다.
void dfs(int start, int prev) {
if (dp[start][true] > dp[start][false] && prevA[prev] == false) {
res1.push_back(start+1);
prevA[start] = true;
}
for (int i = 0; i < arr2[start].size(); ++i) {
int there = arr2[start][i];
if (there != prev) {
dfs(there, start);
}
}
}
📃 소스 코드 :
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N;
vector<vector<int>> arr;
vector<vector<int>> arr2;
vector<int> weight;
vector<vector<int>> dp;
vector<bool> visited;
vector<int> res1;
vector<bool> prevA;
void setTree(int root) {
for (int i = 0; i < arr[root].size(); ++i) {
int there = arr[root][i];
if (!visited[there]) {
visited[there] = true;
arr2[root].push_back(there);
setTree(there);
}
}
}
int getSet(int number, bool inv) {
int &ret = dp[number][inv];
if (ret != -1) {
return ret;
}
if (inv) {
ret = weight[number];
for (int i = 0; i < arr2[number].size(); ++i) {
int there = arr2[number][i];
ret += getSet(there, false);
}
}
else {
ret = 0;
for (int i = 0; i < arr2[number].size(); ++i) {
int there = arr2[number][i];
ret += max(getSet(there, true), getSet(there, false));
}
}
return ret;
}
void dfs(int start, int prev) {
if (dp[start][true] > dp[start][false] && prevA[prev] == false) {
res1.push_back(start+1);
prevA[start] = true;
}
for (int i = 0; i < arr2[start].size(); ++i) {
int there = arr2[start][i];
if (there != prev) {
dfs(there, start);
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; ++i) {
int w;
cin >> w;
weight.push_back(w);
}
arr = vector<vector<int>>(N);
arr2 = vector<vector<int>>(N);
dp = vector<vector<int>>(N, vector<int>(2, -1));
visited = vector<bool>(N, false);
int a, b;
while (!cin.eof()) {
cin >> a >> b;
arr[a - 1].push_back(b - 1);
arr[b - 1].push_back(a - 1);
}
visited[0] = true;
setTree(0);
prevA = vector<bool>(N, false);
bool ok = false;
int answer = max(getSet(0, true), getSet(0, false));
if (answer== 0) {
cout << 0 << endl;
}
else {
cout << answer;
dfs(0, 0);
sort(res1.begin(), res1.end());
for (int i = 0; i < res1.size(); ++i) {
cout << res1[i] << " ";
}
}
for (int i = 0; i < dp.size(); ++i) {
cout << dp[i][0] << " : " << dp[i][1] << endl;
}
}궁금하신 것이 있으시면 언제든지 댓글 달아주세요!

'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [프로그래머스] 프렌즈4블록 (0) | 2020.08.30 |
|---|---|
| [백준] 15684번 - 사다리 조작 (0) | 2020.08.20 |
| [백준] 2580번 - 스도쿠 (0) | 2020.08.17 |
| [백준] 14888번 - 연산자 끼워넣기 (0) | 2020.08.13 |
| [백준] 9205번 - 맥주 마시면서 걸어가기 (카스텐라우프) (0) | 2020.08.10 |
