
https://www.acmicpc.net/problem/15684
15684번: 사다리 조작
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선
www.acmicpc.net
💡 원리
문제의 정답 비율을 보고 풀기에 무서웠던 문제였다.
하지만 문제를 잘 읽고, 잘 생각하면서 코드를 짜면 생각보다 쉽게 풀어지는 문제였다.
이 문제는 쉽게 주변에서 볼 수 있는 사다리 타기 게임과 같은 원리의 문제이다.
하지만 사다리 타기 게임과 다른 점은 두 가로선이 연속하면 안 되는 것에 있었다.
( 이 조건은 이 문제를 정말 쉽게 풀 수 있게 해주는 조건이였다.)
이 문제의 가장 중요한 기능은 가로선을 3개까지 추가하면서 값을 도출해내는 것이다.
가로선을 추가하는 모든 경우의 수를 일일이 탐색하기 위해서는 백트래킹 방법을 이용할 수 있다.
우선 백트래킹 방식으로 풀기 위해 그래프를 이용할 것이기 때문에 세로선과 가로선을 그래프로 표현을 해주자.
그래프를 만들기 위해서 행의 개수와 열의 개수를 파악을 해야 하는데,
행과 열의 개수는 아래와 같다.
🔗 행의 개수 : 가로의 개수 +2 -> H+2 (시작점과 도착점을 포함하기 때문에 +2)
🔗 열의 개수 : 시작점의 개수 ( 세로의 개수 ) -> N

사다리를 그래프로 표현을 해줬으니 간단하게 풀어질 것이다.
이런 조건으로 그래프를 만들어주고 가로선을 추가하기 전
즉, 최종 함수를 만들기 전에 우선 사다리 타기 기능을 제대로 할 수 있도록 해주는 함수를 만들어봤다.
※ 이렇게 기본적인 함수를 먼저 만들어준 후 테스트를 해주면, 나중에 주요 함수를 만들 때 간편해질 수 있습니다.
✏️ 사다리 게임 기능 함수
bool ladder_check() {
bool ok = false;
for (int i = 0; i < N; ++i) {
int x = 0; int y = i;
int mvx = 1; int mvy = 0;
int dx = x + mvx; int dy = y + mvy;
while (dx < H + 1) {
if (arr[dx][dy] != 0) {
if (dy + 1 < N && arr[dx][dy + 1] == arr[dx][dy]) {
dy = dy + 1;
}
else if (dy - 1 >= 0 && arr[dx][dy - 1] == arr[dx][dy]) {
dy = dy - 1;
}
}
dx = dx + mvx;
}
if (i == dy) {
ok = true;
}
else {
ok = false;
break;
}
}
return ok;
}위 함수는 각 시작점에서 사다리 타기 한 후 도착점들이 자신의 시작점과 똑같이 도착했는지 여부를 판단해준다.
이제 사다리 타기 기능을 완성했으니, 가로선을 추가해주는 메인 함수를 만들어보자.
가로선은 최대 3개까지 추가할 수 있다. 그렇기 때문에 깊이(길이)를 매개변수로 하고,
길이가 3 이하까지 백트래킹을 하면서 최솟값이 나올 때까지 만들어질 수 있는 모든 경우의 수를 나오게 하였다.
다른 백트래킹 문제와 같은 방식으로, 가로선을 만들 수 있는 부분에서 visited 함수를 만들어 방문 여부를 파악한 후,
총 3개까지 백트래킹을 하였다.
※ 주의할 점 :
1. 그래프를 만들어 주고 사다리를 설치할 때, 연속되는 사다리를 만들거나 탐색하지 않도록 다른 수로 저장해 주자!
만약 숫자가 1로 같다면, 연속되는 사다리를 설치한 꼴이 될 것이다.
arr[i + 1][j] = len + 1 + M;
arr[i + 1][j + 1] = len + 1 + M;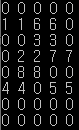

2. 시간 초과가 나지 않도록 최솟값보다 len의 길이가 크다면 더 이상 백트래킹을 하지 않도록 해주자!
if (minNum > len) { }
이렇게 시간 초과가 나오지 않도록 백트래킹 함수까지 완성했다면, 이 문제는 쉽게 풀릴 것이다.
📃 구현 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M, H;
vector<vector<int>> arr;
vector<vector<bool>> visited;
int minNum = 4;
vector<int> answer;
int cnt = 1;
bool check() {
bool ok = false;
for (int i = 0; i < N; ++i) {
int x = 0; int y = i;
int mvx = 1; int mvy = 0;
int dx = x + mvx; int dy = y + mvy;
while (dx < H + 1) {
if (arr[dx][dy] != 0) {
if (dy + 1 < N && arr[dx][dy + 1] == arr[dx][dy]) {
dy = dy + 1;
}
else if (dy - 1 >= 0 && arr[dx][dy - 1] == arr[dx][dy]) {
dy = dy - 1;
}
}
dx = dx + mvx;
}
if (i == dy) {
ok = true;
}
else {
ok = false;
break;
}
}
return ok;
}
void dfs(int len,int x) {
if (minNum > len) {
if (check()) {
for (int i = 0; i < H + 2; ++i) {
for (int j = 0; j < N; ++j) {
cout << arr[i][j] << " ";
}
cout << endl;
}
minNum = min(minNum, len);
}
if (len == 3) {
return;
}
else {
vector<vector<int>> tmp = arr;
for (int i = x; i < H; ++i) {
for (int j = 0; j < N - 1; ++j) {
if (!visited[i][j] && !visited[i][j + 1]) {
visited[i][j] = true;
visited[i][j + 1] = true;
arr[i + 1][j] = len + 1 + M;
arr[i + 1][j + 1] = len + 1 + M;
dfs(len + 1, i);
visited[i][j] = false;
visited[i][j + 1] = false;
arr = tmp;
}
}
}
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N >> M >> H;
arr = vector<vector<int>>(H + 2, vector<int>(N, 0));
visited = vector<vector<bool>>(H, vector<bool>(N, false));
for (int i = 0; i < M; ++i) {
int a, b;
cin >> a >> b;
arr[a][b - 1] = cnt;
arr[a][b] = cnt;
visited[a - 1][b - 1] = true;
visited[a - 1][b] = true;
cnt += 1;
}
dfs(0, 0);
if (minNum < 4) { cout << minNum; }
else { cout << -1; }
}궁금하신 것이 있으시면 언제든지 댓글 달아주세요!

'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [백준] 2213번 - 트리의 독립집합 (0) | 2020.09.07 |
|---|---|
| [프로그래머스] 프렌즈4블록 (0) | 2020.08.30 |
| [백준] 2580번 - 스도쿠 (0) | 2020.08.17 |
| [백준] 14888번 - 연산자 끼워넣기 (0) | 2020.08.13 |
| [백준] 9205번 - 맥주 마시면서 걸어가기 (카스텐라우프) (0) | 2020.08.10 |
