
☞ 세그먼트 트리란 이름 그대로 저장된 자료를 적절히 구간별로 전처리해 그들에 대한 질의들을 빠르게 대답할 수 있도록 해주는 트리입니다. 예를 들어 A={1,2,3,4,5}에서 [2,4] 구간의 최소치를 알고 싶다면 해당 배열을 순회하며 찾는 방법도 있지만, 해당 배열을 전처리해 세그먼트 트리를 생성해 더욱 더 빠르게 구현 할 수 있습니다.
A배열을 세그먼트 트리로 바꾼 후 -> 아래처럼 구간별로 나눠 세그먼트 트리를 만들 수 있다.
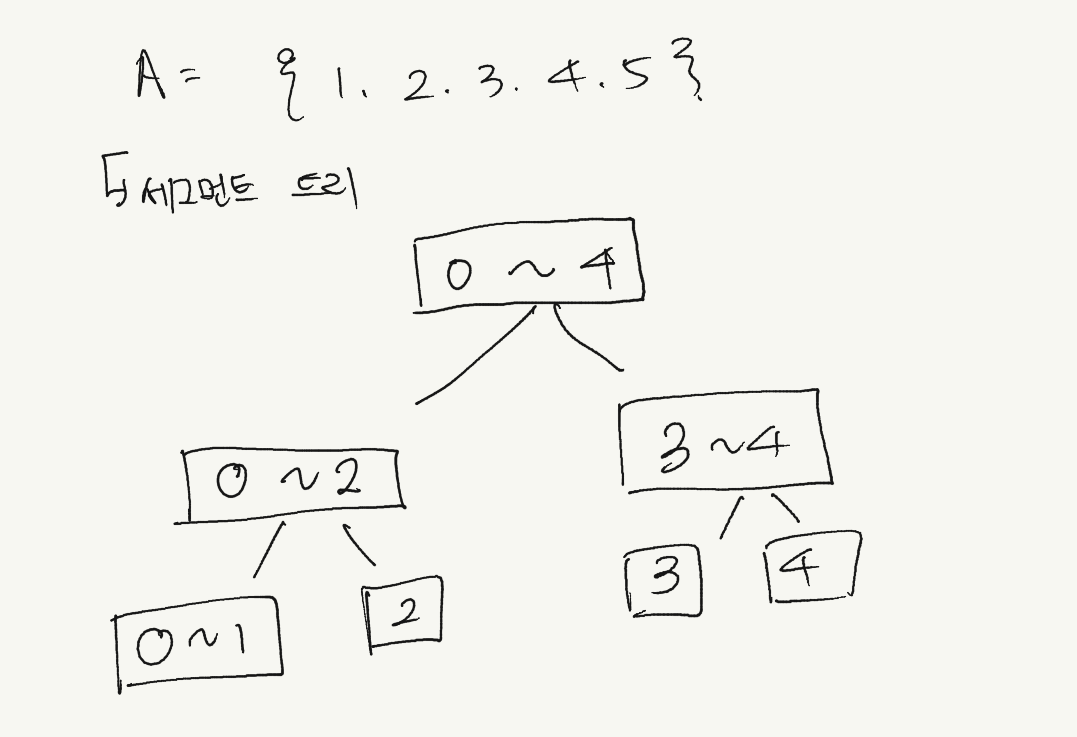
☞ 이렇게 이론적으로만 설명했지만, 코드 구현에 많은 어려움이 있을 수 있습니다.
그래서 세그먼트 트리 문제의 한 유형인 구간 최소 쿼리(range minimum query,RMQ)를 구현해보겠습니다.
※ 여기서 중요한 점은 세그먼트 트리에 초기 크기를 설정해줘야하는데 가장 이상적인 사이즈는 n을 2의 거듭제곱으로 올림한 뒤 2를 곱하는 사이즈입니다. 하지만 매번 이렇게 하면 귀찮으므로 메모리가 조금 낭비하더라도 4*n을 크기로 사용 할 수 있습니다.
구간을 초기화 할 때 구간 최소 쿼리이므로 각 노드에는 그 구간에 맞는 최소 값이 있어야 합니다. 따라서 아래 그림과 같이 세그먼트 트리를 만들어 줘야 합니다. (A= { 1, 2, 1, 2, 3, 1, 2, 3, 4})

☞ 소스 코드 (참고 : 프로그래밍 대회에서 배우는 알고리즘 문제해결 전략)
struct RMQ {
int n; // 배열의 길이
vector<int> rangeMin; // 각 구간의 최소치
RMQ(vector<int> array) {
n = array.size();
rangeMin.resize(n * 4);
init(array, 0, n - 1, 1);
}
// 세그먼트 트리 초기 값 설정
int init(vector<int> array, int left, int right, int node) {
if (left == right) {
return rangeMin[node] = array[left];
}
int mid = (left + right) / 2;
int leftMin = init(array, left, mid, node * 2);
int rightMin = init(array, mid + 1, right, node * 2 + 1);
return rangeMin[node] = min(leftMin, rightMin);
}
// 세그먼트 트리를 이용해 left, right 구간의 최소 값 도출하기 위한 함수
int query(int left, int right, int node, int nodeLeft, int nodeRight) {
if (right < nodeLeft || left > nodeRight) return INF;
if (left <= nodeLeft && nodeRight <= right) return rangeMin[node];
int mid = (nodeLeft + nodeRight) / 2;
return min(query(left, right, node * 2, nodeLeft, mid), query(left, right, node * 2 + 1, mid + 1, nodeRight));
}
// query함수를 위한 간략해 놓은 인터페이스 함수
int query(int left, int right) {
return query(left, right, 1, 0, n - 1);
}
// 세그먼트 트리의 index의 값을 newValue 값으로 변경하기 위한 함수
int update(int index, int newValue, int node, int nodeLeft, int nodeRight) {
if (index < nodeLeft || index > nodeRight) return rangeMin[node];
if (nodeLeft == nodeRight) return rangeMin[node] = newValue;
int mid = (nodeLeft + nodeRight) / 2;
return rangeMin[node] = min(update(index, newValue, node * 2, nodeLeft, mid), update(index, newValue, node * 2+1, mid + 1, nodeRight));
}
//update함수를 위한 간략해 놓은 인터페이스 함수
int update(int index, int newValue) {
return update(index, newValue, 1, 0, n - 1);
}
};※ 함수 시간 복잡도
구간 트리 초기화 - init() : O(n)
구간 트리의 질의 처리 - query() : O(logn)
☞ RMQ 구현을 통해 세그먼트 트리의 원리에 대해 조금이나마 익숙해질 수 있을 것입니다. 이 RMQ 구조체만 잘 익힌다면 각 구간의 최대 값을 구하는 문제와 같은 세그먼트 트리를 활용한 문제를 쉽게 풀 수 있을 것입니다!
궁금하신 것이 있으시다면 댓글로 남겨주세요!~

'Algorithm > Theory' 카테고리의 다른 글
| 프림 알고리즘 (Prim Algorithm) (0) | 2020.07.29 |
|---|---|
| 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2020.07.29 |
| Union-Find, Disjoint Set (유니온-파인드, 상호 배타적 집합) (0) | 2020.06.22 |
| 벨만-포드 알고리즘 (Bellman-Ford Algorithm) (0) | 2020.05.19 |
| [c++] 입력은 여러 개의 테스트 케이스로 이루어져 있다. (0) | 2020.02.04 |
