
☞ Union-Find 란?
상호 배타적인 부분 집합(Disjoint Set)들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조
Union-Find에는 자료 구조에 명칭에 맞게 연산이 초기화(init), 합치기(union) 그리고 찾기(find)로 이루어져 있습니다.
초기화 : n개의 원소가 각각의 집합에 포함되어 있도록 초기화
합치기 연산 : 두 원소가 주어질 때 이들이 속한 두 집합을 하나로 합치는 연산
찾기 연산 : 어떤 원소가 주어질 때 이 원소가 속한 집합을 반환하는 연산
☞ 상호 배타적 집합을 표현하는 방법은 2가지가 있는데,
첫번째는 배열입니다.
하지만 배열로 표현을 하면 합치기 연산에 드는 시간이 많이 걸리기 때문에 Union-Find 자료 구조 특성 상 효율적이지 못합니다. 그래서 Union-Find 자료 구조는 대부분 트리로 표현됩니다.
두번째는 트리입니다.
한 집합에 속하는 원소들을 하나의 트리로 묶어 줍니다. 이때 원소가 같은 트리에 속해 있는지 확인하는 가장 직관적인 방법은 각 원소가 포함된 트리의 루트를 찾은 뒤 이들이 같은지 비교하는 것이며, 트리와 루트는 항상 1:1 대응되기 때문에, 루트가 같다면 두 노드가 같은 트리에 속해 있음을 알 수 있습니다.
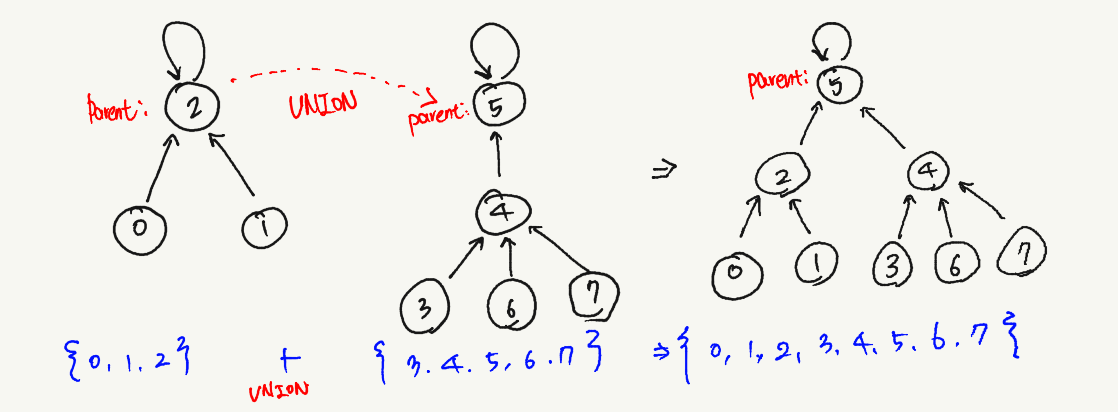
자 그럼, 유니온-파인드 자료 구조를 코드로 구현해보겠습니다.
☞ 우선, 코드로 구현하기 전 유니온-파인드를 더 효율적으로 구현할 수 있는 최적화를 해보겠습니다.
1. 랭크에 의한 합치기(Union-by-rank) 최적화 : 트리에 한쪽에만 붙을 수 있어 한쪽으로 기울어진 트리가 만들어지는 문제점입니다. 이때 find 연산과 union연산이 트리의 높이 만큼의 복잡도가 나오기 떄문에 매우 비효율적입니다.
이를 해결하기 위해 랭크에 의한 합치기(Union-by-rank) 최적화를 사용해 항상 높이가 더 낮은 트리를 더 높은 트리 밑에 집어넣을 수 있습니다.
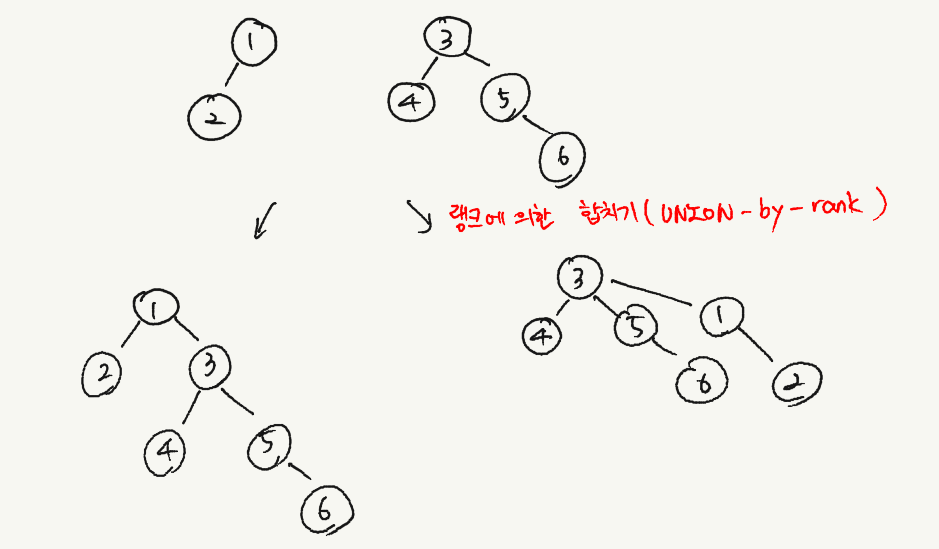
2. 경로 압축(path compression) 최적화 : find 연산에서 원소의 루트를 찾아내는 과정에서, parent 포인터를 루트로 바꿔 버리면 다음에 find 연산이 호출될때 경로를 따라 다시 올라갈 필요 없어 바로 루트를 찾을 수 있도록 해주는 최적화입니다.
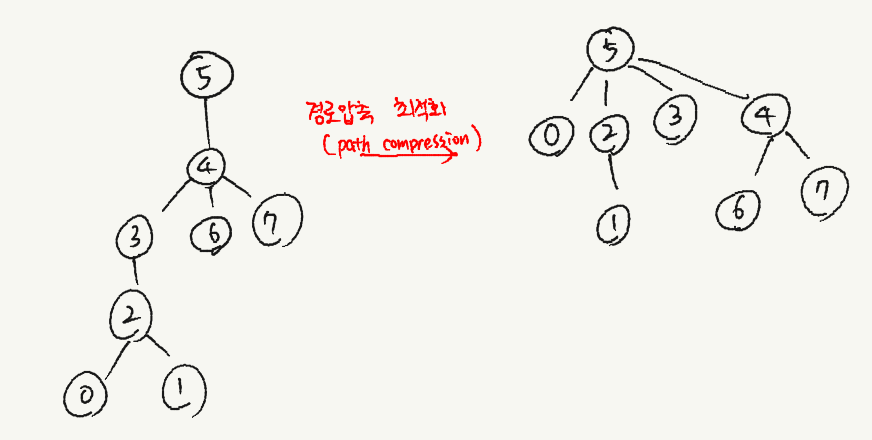
그럼 이 2가지의 최적화를 반영해서 코드를 구현해보겠습니다.
☞ 소스 코드 :
struct OptimizedDisjointSet {
vector<int> parent, rank; //rank -> 1번째 최적화를 위한 변수
OptimizedDisjointSet(int n) : parent(n), rank(n, 1) {
for (int i = 0; i < n; ++i)
parent[i] = i;
}
//Find 연산
int find(int u) {
if (u == parent[u]) return u;
return parent[u] = find(parent[u]); // 2번째 최적화를 위해 find의 return 값을 parent[u]에 다시 넣어준다.
}
//Union 연산
void merge(int u, int v) {
u = find(u); v = find(v);
if (u == v) return;
if (rank[u] > rank[v]) swap(u, v); // 1번째 최적화를 위한 swap
parent[u] = v;
if (rank[u] == rank[v]) ++rank[v];
}
};궁금하신 것이 있으시면 언제든지 댓글 달아주세요!

'Algorithm > Theory' 카테고리의 다른 글
| 프림 알고리즘 (Prim Algorithm) (0) | 2020.07.29 |
|---|---|
| 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2020.07.29 |
| 세그먼트 트리 (구간 트리, Segment Tree) (0) | 2020.05.25 |
| 벨만-포드 알고리즘 (Bellman-Ford Algorithm) (0) | 2020.05.19 |
| [c++] 입력은 여러 개의 테스트 케이스로 이루어져 있다. (0) | 2020.02.04 |
