728x90


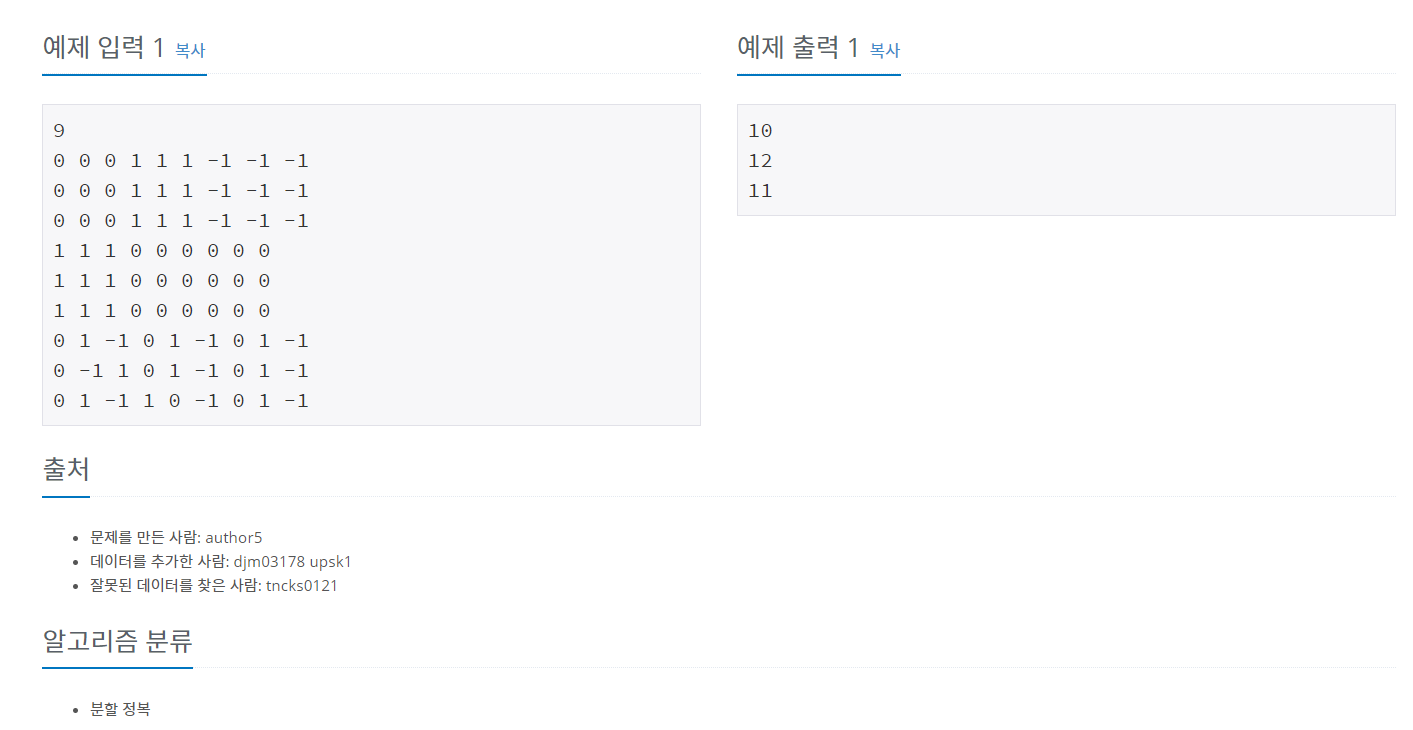
3의 제곱만큼 늘어나는 종이에서 같은 숫자를 가진 3^n 의 종이의 개수 -1,0,1를 각각 찾는 문제이다.
처음에 브루트포스를 접근을 하려 했지만, 시간이 어마어마하게 나올 것 같아서 분할 정복을 도입해봤다. 다행히 문제에 3^N 으로 늘어나며, 종이를 자를때도 3^N이라는 규칙에 맞게 자르기 때문에 쉽게 규칙을 찾을 수 있었다.
우선 findPaper 함수를 만들어 NXN의 크기부터 검사를 하도록 하고, 같은 숫자로 다 이루어지지 않을 시에
(N/3)X(N/3)으로 N개만큼 분할해서 다시 구하도록 재귀 함수를 구현해주었다.
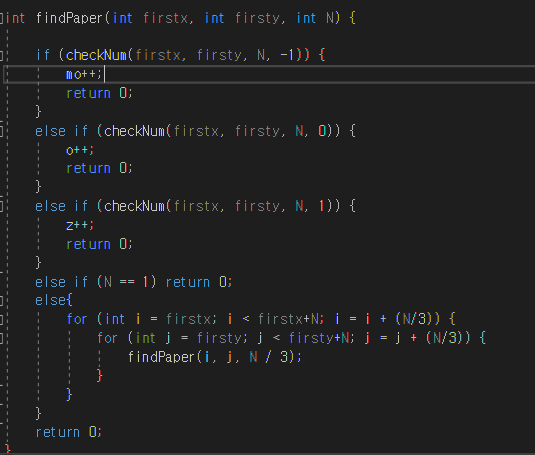
firstx와 firsty를 이용해 규칙에 맞게 그 종이를 구성하는 첫번째 인자만 가져올 수 있도록 해주었다.
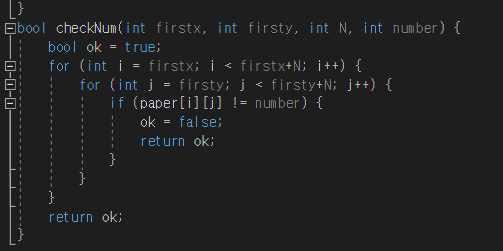
또한 구성된 숫자를 검사할때는 checkNum 함수를 이용해서 쉽게 검사를 해줄 수 있도록 해주며, 쉽게 종이에 구성된 숫자를 모두 확인을 해주었다.

개선해야할 점: 처음에는 어떻게 접근을 해야할지 난감했었지만, 그림을 그려가면 쉽게 접근을 해주니 괜찮았던 것 같다.
#include <iostream>
#include <vector>
#include <math.h>
#include <algorithm>
using namespace std;
bool checkNum(int firstx, int firsty, int N, int number);
int N;
int mo = 0; int o = 0; int z = 0;
int paper[2200][2200];
int findPaper(int firstx, int firsty, int N) {
if (checkNum(firstx, firsty, N, -1)) {
mo++;
return 0;
}
else if (checkNum(firstx, firsty, N, 0)) {
o++;
return 0;
}
else if (checkNum(firstx, firsty, N, 1)) {
z++;
return 0;
}
else if (N == 1) return 0;
else{
for (int i = firstx; i < firstx+N; i = i + (N/3)) {
for (int j = firsty; j < firsty+N; j = j + (N/3)) {
findPaper(i, j, N / 3);
}
}
}
return 0;
}
bool checkNum(int firstx, int firsty, int N, int number) {
bool ok = true;
for (int i = firstx; i < firstx+N; i++) {
for (int j = firsty; j < firsty+N; j++) {
if (paper[i][j] != number) {
ok = false;
return ok;
}
}
}
return ok;
}
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cin >> paper[i][j];
}
}
findPaper(0, 0, N);
cout << mo << endl;
cout << o << endl;
cout << z ;
}
소스코드 : https://github.com/withseungryu/Algorithms/blob/master/BackJoon/1780.cpp
728x90
반응형
'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [백준] 10942번 - 팰린드롬? (2) | 2020.02.16 |
|---|---|
| [백준] 1725번 히스토그램 & [프알문] 울타리 잘라내기 (0) | 2020.01.29 |
| [백준] 1012번 유기농 배추 (0) | 2020.01.23 |
| [백준] 2503번 숫자 야구 (0) | 2020.01.14 |
| 프.알.문-무식하게 풀기<소풍> (0) | 2019.01.11 |
