

이번 문제는 팰린드롬이라는 생소한 단어가 나왔는데, 문제에서 팰린드롬의 정의를 해주지 않아 인터넷에 팰린드롬이라는 단어를 찾아봤습니다.

위키백과에서는 palindrome을 회문이라 했으며, 회문이란 숫자나 문자를 정방향으로 읽어도, 거꾸로 읽어도 같은 숫자나 문자를 말합니다.
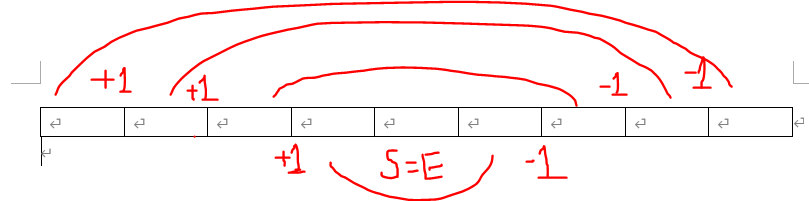
처음에 이 문제를 해결하기 위해서 각 위치에 맞는 짝을 찾아 비교하기 위해 규칙을 찾아보았는데, 따로 규칙을 찾을 필요없이 우리가 S, E를 선택했기 때문에 (S+i) = (E-i) 라는 규칙을 쉽게 생각 할 수 있었습니다. 그리고 이 문제 조건에서 시간 제한을 0.5초를 두었기 때문에 Dynamic programming을 이용해야 함을 알 수 있었습니다.
int palin(int s, int e) {
if (s >= e) {
return 1;
}
int& ret = cache[s][e];
if (ret != -1) return ret;
if (board[s] == board[e]) {
return ret = palin(s + 1, e - 1);
}
else { return 0; }
}
동적프로그래밍을 살려주기 위해 cache 배열을 만들어 palin(x,y)를 cache[x][y]에 저장을 해두어 나중에 palin(x,y)를 만났을 때 따로 비효율적으로 다시 한번 순회하지 않고 바로 cache에서 가져와 쓸 수 있도록 해주었습니다.!!
※시간초과 나는 분께! :
하지만 이렇게 해도 계속 시간초과가 나와서 당황했는데, 시간 초과가 나오는 이유를 곰곰히 생각해보다가 시간을 많이 잡는 cin 과 cout을 scanf와 printf 로 바꿔보았는데, 다행히 시간 초과가 안나오고 성공 할 수 있었습니다.
◆ cout , cin 사용 코드
int main() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> board[i];
}
memset(cache, -1, sizeof(cache));
int M;
cin >> M;
while (M--) {
int S, E;
cin >> S >> E;
res.push_back(palin(S, E));
}
for (int i = 0; i < (int)res.size(); ++i) {
cout << res[i] << endl;
}
}◆ printf , scanf 사용 코드
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; i++) {
scanf("%d", &board[i]);
}
memset(cache, -1, sizeof(cache));
int M;
cin >> M;
while (M--) {
int S, E;
scanf("%d %d", &S, &E);
res.push_back(palin(S, E));
}
for (int i = 0; i < (int)res.size(); ++i) {
printf("%d\n", res[i]);
}
}전체코드 :
#include <iostream>
#include <memory.h>
#include <vector>
using namespace std;
int N;
int board[2001];
int cache[2001][2001];
vector<int> res;
int palin(int s, int e) {
if (s >= e) {
return 1;
}
int& ret = cache[s][e];
if (ret != -1) return ret;
if (board[s] == board[e]) {
return ret = palin(s + 1, e - 1);
}
else { return 0; }
}
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; i++) {
scanf("%d", &board[i]);
}
memset(cache, -1, sizeof(cache));
int M;
cin >> M;
while (M--) {
int S, E;
scanf("%d %d", &S, &E);
res.push_back(palin(S, E));
}
for (int i = 0; i < (int)res.size(); ++i) {
printf("%d\n", res[i]);
}
}
소스 코드 :https://github.com/withseungryu/Algorithms/blob/master/BackJoon/Dynamic%20Programming/10942.cpp
withseungryu/Algorithms
Algorithms study. Contribute to withseungryu/Algorithms development by creating an account on GitHub.
github.com
궁금하신 것이 있으시다면 댓글로 남겨주세요!~

'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [백준] 2178번 - 미로 탐색 (0) | 2020.04.29 |
|---|---|
| [백준] 11266번 - 단절점 (Articulation Point) (0) | 2020.04.29 |
| [백준] 1725번 히스토그램 & [프알문] 울타리 잘라내기 (0) | 2020.01.29 |
| [백준] 1780번 종이의 개수 (0) | 2020.01.25 |
| [백준] 1012번 유기농 배추 (0) | 2020.01.23 |
