


이 문제의 유형은 깊이 유형 탐색을 통해 절단점을 찾는 것이다.
절단점이란? - 무향그래프에서 어떠한 점의 인접한 간선들을 모두 지웠을 때 -> 해당 Component가 2개로 나뉠때의 어떤한 점이 절단점
● 어떠한 점이 절단점이 될 수 있을 조건 - 2가지
1) 기준점이 u일때 자손 v들이 역방향 간선을 통해 u의 선조들로 올라갈 수 있을 때
if (!root && subtree >= discovered[here]) {
isCutVertex[here] = true;
}subtree = isCutVertexDfs(there, false) 의 의미는 현재 점의 역행 간선이 존재 할 때 자신의 선조 어느 곳까지 올라 갈 수 있는지 보여준다. 따라서 subtree는 discovered를 저장하기 때문에 subtree가 낮게 나올 수록 더 빨리 발견되어진 선조, 즉 더 높은 선조까지 올라 갈 수 있음을 보인다.
따라서 subtree >= discovered[here]의 의미는 현재 점이 here 보다 더 높은 선조까지 올라 갈 수 없음을 알려주는 조건이다.
2) u가 루트일 때 자손이 2개 이상 존재 할때
if (root) {
isCutVertex[here] = (children >= 2);
}현재 점이 루트일 때 자식노드가 2개 이상이면 절단점이 될 수 있다.
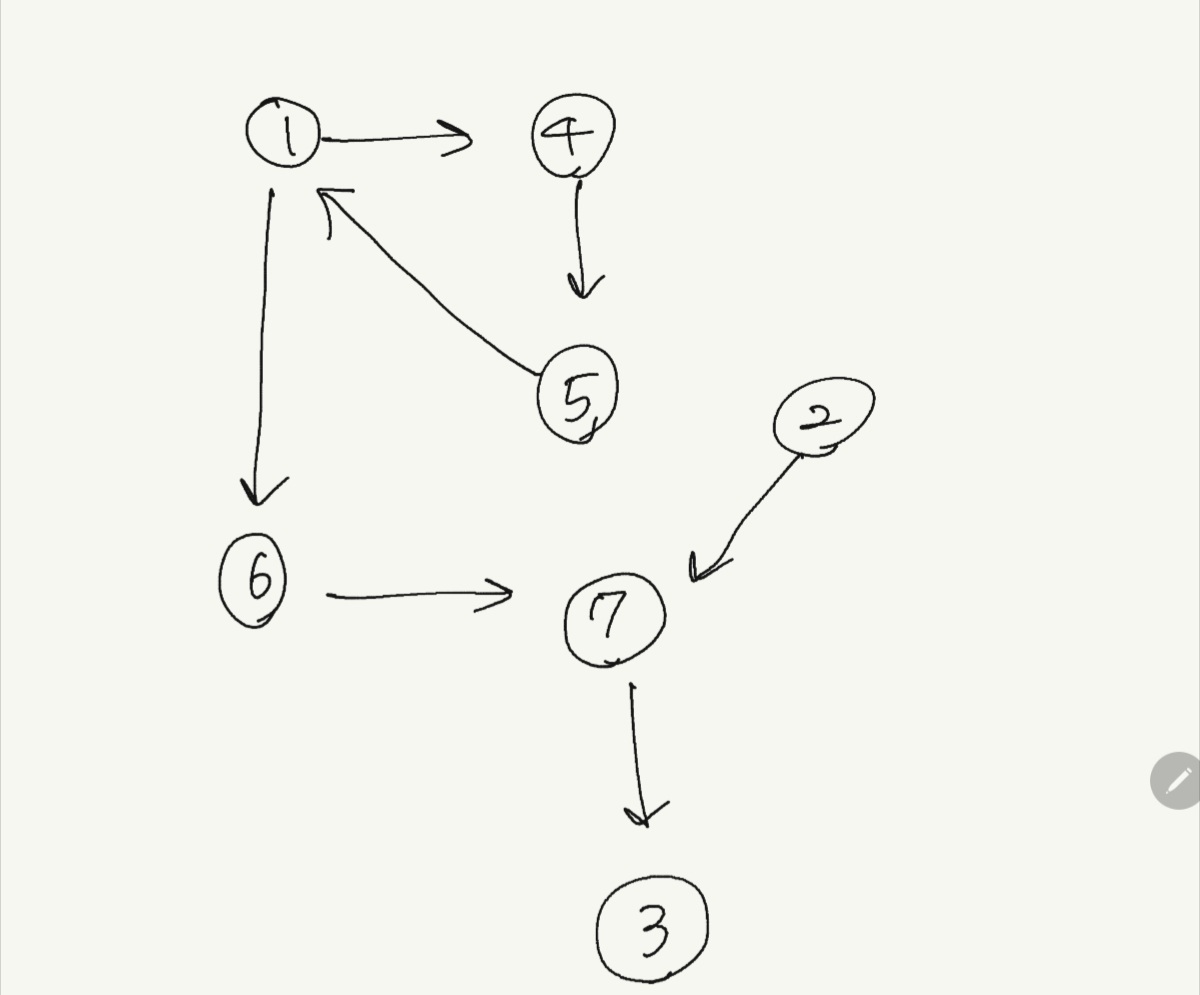
1 = 1에서 6과 4로 dfs 할 때 1보다 더 높은 선조로 갈 수 있는 역행 간선 존재X -> o
2 = 자식 노드 2개 이상X -> x
3 = 자식 노드 2개 이상X -> x
4 = 자식 노드인 5가 4의 선조인 1까지 갈 수 있는 역행 간선 존재 -> x
5 = 자식 노드인 1이 5의 선조인 4까지 갈 수 있는 역행 간선 존재 -> x
6 = 자식 노드 중 6의 선조로 가는 역행 간선 존재 x -> o
7 = 자식 노드 중 7의 선조로 가는 역행 간선 존재 x -> o
따라서 1, 6, 7이 나올 수 있다.
이러한 원리로 위 2개의 조건과 dfs를 잘 섞어 코드를 짤 수 있습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int v, e;
vector<vector<int>> adj;
vector<int> discovered;
vector<bool> isCutVertex;
int counter=0;
int cnt = 0;
int isCutVertexDfs(int here, bool root) {
discovered[here] = ++counter;
int ret = discovered[here];
int children = 0;
for (int i = 0; i < adj[here].size(); ++i) {
int there = adj[here][i];
if (discovered[there] == -1) {
++children;
int subtree = isCutVertexDfs(there, false);
if (!root && subtree >= discovered[here]) {
isCutVertex[here] = true;
}
ret = min(ret, subtree);
}
else {
ret = min(ret, discovered[there]);
}
}if (root) {
isCutVertex[here] = (children >= 2);
}
return ret;
}
int main() {
cin >> v >> e;
adj = vector<vector<int>>(v + 1);
for (int i = 0; i < e; ++i) {
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
discovered = vector<int>(v + 1, -1);
isCutVertex = vector<bool>(v + 1, false);
for (int i = 1; i <= v; ++i) {
if(discovered[i] == -1)
isCutVertexDfs(i, true);
}
for (int i = 0; i < (int)isCutVertex.size(); ++i) {
if (isCutVertex[i])
cnt++;
}
cout << cnt << endl;
for (int i = 0; i < (int)isCutVertex.size(); ++i) {
if (isCutVertex[i])
cout << i << " ";
}
}
소스코드 : https://github.com/withseungryu/Algorithms
withseungryu/Algorithms
Algorithms study. Contribute to withseungryu/Algorithms development by creating an account on GitHub.
github.com
궁금하신 것이 있으시다면 댓글로 남겨주세요!~

'Algorithm > Problem and Strategies' 카테고리의 다른 글
| [백준] 5014번 - 스타트링크 (0) | 2020.04.29 |
|---|---|
| [백준] 2178번 - 미로 탐색 (0) | 2020.04.29 |
| [백준] 10942번 - 팰린드롬? (2) | 2020.02.16 |
| [백준] 1725번 히스토그램 & [프알문] 울타리 잘라내기 (0) | 2020.01.29 |
| [백준] 1780번 종이의 개수 (0) | 2020.01.25 |
